Running GeoHiSSE
Daniel Caetano and Jeremy M. Beaulieu
GeoHiSSE-vignette.RmdAs of version 1.8.7, we provide a new set of functions that execute
more complex and potentially faster version of the GeoHiSSE model
described by Caetano et al. (2018). One of the main differences here is
that the model allows up to 10 hidden categories, and implements a more
efficient means of carrying out branch calculations. Specifically, we
break up the tree into sets of branches whose branch calculations are
independent of one another. We then carry out all descendent branch
calculations simultaneously, combine the probabilities based on their
shared ancestry, then repeat for the next set of descendent branches. In
testing, we’ve found that as the number of taxa increases, the
calculation becomes much more efficient. For instance, with 100,000
tips, a single tree traversal with the canonical GeoSSE model in the
original code took 10 minutes, whereas in GeoHiSSE the same
traversal took about 30 seconds. Note this function now replaces the
original version of GeoHiSSE, but we retained its
functionality (see GeoHiSSE.old()).
There are a couple major differences with this version of
GeoHiSSE() that users should be aware. First, while this
version allows for cladogenetic events to be turned off (i.e.,
assume.cladogenetic=FALSE), it does not revert to a
three-state MuSSE model as it does in GeoHiSSE. Instead, no
lineage speciation and extinction are allowed in the widespread state,
only transitions out of it. If a three-state MuSSE model is needed, we
direct users to read the vignette on how to generate a three-state model
in MuHiSSE (see Running a Multistate HiSSE model vignette).
The other main difference is that, like hisse, we employ
a modified optimization procedure. Rather than optimizing birth and
death separately, GeoHisse optimizes orthogonal
transformations of these variables: we let \(\tau\) define net turnover, and we let
\(\epsilon\) define the extinction
fraction. However, these transformations are slightly more complicated
due to the dynamics associated with the widespread taxa. For a
geographic-based model, we define turnover as,
\[\tau_{00i} = s_{00i} + x_{00i}\] \[\tau_{11i} = s_{11i} + s_{11i}\] \[\tau_{01i} = s_{00i} + s_{11i} + s_{01i}\]
We define extinction fraction as
\[\epsilon_{00i} = x_{00i} / s_{00i}\] \[\epsilon_{11i} = x_{11i} / s_{11i}\]
and because there is no lineage extinction for widespread ranges, \(\epsilon_{01i} = 0\).
It is straightforward to convert back to original speciation and extinction, \(s\) and \(x\), respectively:
\[s_{00i} = \tau_{00i} / (1 + \epsilon_{00i})\] \[s_{11i} = \tau_{11i} / (1 + \epsilon_{11i})\] \[s_{01i} = \tau_{01i} - s_{00i} - s_{11i}\]
\[x_{00i} = (\tau_{00i}*\epsilon_{00i}) / (1 + \epsilon_{00i})\] \[x_{11i} = (\tau_{11i}*\epsilon_{11i}) / (1 + \epsilon_{11i})\]
Also, note that the output from GeoHiSSE can be used and
processed using available functions. For example, the output can
automatically be used to obtain model averages (i.e.,
GetModelAveRates()), generate estimates of the uncertainty
in the parameter estimates (i.e., SupportRegionGeoSSE()),
calculate the marginal probabilities for states at nodes (i.e.,
MarginReconGeoSSE()), and plotting the rate variation on
the tree (i.e., plot.geohisse.states()). Users are
encouraged to read other vignettes and help pages provided for more
information. For more conceptual discussions of these functions and
ideas, readers are also encouraged to read Caetano et al. (2018).
Getting started
The GeoHiSSE models can be used to infer ancestral ranges, rates of dispersion and extirpation, as well as testing hypotheses about range-dependent diversification processes. The main difference between GeoSSE and GeoHiSSE is that here we implement models that allow for diversification rate variation both within and between geographical areas. Such models are more adequate to empirical data then homogeneous diversification rates implied by GeoSSE (as well as BiSSE). The GeoHiSSE models belong to the same category of Hidden-Markov models as HiSSE. Thus, the concepts will be familiar to you if you have some experience with HiSSE (and vice-versa).
The best place to install the package with the new functions provided
here is from our github repository using the package
devtools:
library( devtools )
install_github(repo = "thej022214/hisse", ref = "master")Before getting started, be sure to load the hisse and
diversitree packages:
suppressWarnings(library(hisse))## Loading required package: ape## Loading required package: deSolve## Loading required package: GenSA## Loading required package: subplex## Loading required package: nloptrSimulating a range-independent process
We will simulate a phylogenetic tree using neutral geographical ranges, and incorporate two different rates of diversification. Thus, the correct process here is: “rates of diversification vary independently of the geographic ranges”.
We use a simulation here just because it is an easy way to produce data and because we know the underlying diversification process. Otherwise, if you have an empiricial dataset, all the steps we show here apply. Just make sure to substitute the phylogeny and data with your datatset.
## Generate a list with the parameters of the model:
pars <- SimulateGeoHiSSE(hidden.traits = 1, return.GeoHiSSE_pars = TRUE)
pars## $model.pars
## A B
## s01 0 0
## s0 0 0
## s1 0 0
## x0 0 0
## x1 0 0
## d0 0 0
## d1 0 0
##
## $q.01
## 01A 01B
## 01A NA 0
## 01B 0 NA
##
## $q.0
## 0A 0B
## 0A NA 0
## 0B 0 NA
##
## $q.1
## 1A 1B
## 1A NA 0
## 1B 0 NA
##
## attr(,"class")
## [1] "list" "GeoHiSSE_pars"The object pars is a list with all the parameter values
for this model in the correct order and format, but all values are 0.
Thus, we need to populate these parameters with numbers in order to
perform the simulation.
pars$model.pars[,1] <- c(0.1, 0.1, 0.1, 0.03, 0.03, 0.05, 0.05)
pars$model.pars[,2] <- c(0.2, 0.2, 0.2, 0.03, 0.03, 0.05, 0.05)
pars$q.01[1,2] <- pars$q.01[2,1] <- 0.005
pars$q.0[1,2] <- pars$q.0[2,1] <- 0.005
pars$q.1[1,2] <- pars$q.1[2,1] <- 0.005
pars## $model.pars
## A B
## s01 0.10 0.20
## s0 0.10 0.20
## s1 0.10 0.20
## x0 0.03 0.03
## x1 0.03 0.03
## d0 0.05 0.05
## d1 0.05 0.05
##
## $q.01
## 01A 01B
## 01A NA 0.005
## 01B 0.005 NA
##
## $q.0
## 0A 0B
## 0A NA 0.005
## 0B 0.005 NA
##
## $q.1
## 1A 1B
## 1A NA 0.005
## 1B 0.005 NA
##
## attr(,"class")
## [1] "list" "GeoHiSSE_pars"Now we can use the parameters with the same function we applied
before SimulateGeoHiSSE to generate both the data and the
phylogeny.
Here we will set the seed for the simulation, so the outcome of the simulation is always the same. Note that you can change the seed or skip this lines to generate a different, random, dataset.
set.seed(42)
sim.geohisse <- SimulateGeoHiSSE(pars=pars, hidden.traits = 1, x0 = "01A", max.taxa = 500)## [1] "Simulating the phylogeny..."
## [1] "Simulation finished!"
phy <- sim.geohisse$phy
phy$node.labels <- NULL
sim.dat <- data.frame(taxon=sim.geohisse$data[,1], ranges=as.numeric(sim.geohisse$data[,2]))Setting up the models
We will fit a total of four models. Two models with a range-indendent diversification process and two other models in which the range have an effect on the diversification rate of the lineages (each with either one or two rate classes).
Note that the function to estimate the parameters of the model is commented out below. Just uncomment and run to perform the estimate of the models. Here we will load results from a previous estimate.
Models 1 and 2 below do not include hidden classes. For model 1
(mod1), we are assuming equal rates regardless of biogeographic region.
This requires a particular set up of the turnover rate with respect to
the widespread range, which involves removing it from the model.
However, if assume.cladogenetic=TRUE, this does not mean
that we are excluding it from the model. Internally,
GeoHiSSE() will recognize this and set the speciation rate
for, \(s_{01}\), to be equal to the
rate of \(s_{00}\) and \(s_{11}\). Removing the turnover rate for
the widespread range like this is required for any model where the
diversification rates are independent of range evolution:
## Model 1 - Dispersal parameters vary only, no range-dependent diversification.
turnover <- c(1,1,0)
eps <- c(1,1)
trans.rate <- TransMatMakerGeoHiSSE(hidden.traits=0)
trans.rate.mod <- ParEqual(trans.rate, c(1,2))
mod1 <- GeoHiSSE(phy = phy, data = sim.dat, f=c(1,1,1),
turnover=turnover, eps=eps,
hidden.states=FALSE, trans.rate=trans.rate.mod,
turnover.upper=100, trans.upper=10)To conduct a canonical GeoSSE model, where range evolution affects diversification, we add back the turnover rate for the widespread range, such that there are three turnover parameters and two extinction fraction parameters estimated:
## Model 2. Canonical GeoSSE model, range effect on diversification
turnover <- c(1,2,3)
eps <- c(1,1)
trans.rate <- TransMatMakerGeoHiSSE(hidden.traits=0)
trans.rate.mod <- ParEqual(trans.rate, c(1,2))
mod2 <- GeoHiSSE(phy = phy, data = sim.dat, f=c(1,1,1),
turnover=turnover, eps=eps,
hidden.states=FALSE, trans.rate=trans.rate.mod,
turnover.upper=100, trans.upper=10)Models 3 and 4 below each have 2 hidden states. In this case the
models will be more complex. First, we will show how to set up a
range-independent model of diversification. Remember, as with mod1
above, if diversification is independent of range-evolution we must
remove the turnover rate for the widespread range. Again, internally,
GeoSSE() will recognize this (if
assume.cladogenetic=TRUE) and simply set \(s_{01}\) to be equal the rate for \(s_{00}\) and \(s_{11}\).
## Model 3. GeoHiSSE model with 1 hidden trait, no range-dependent diversification.
## Note below how parameters vary among hidden classes but are the same within each
## hidden class.
turnover <- c(1,1,0,2,2,0)
eps <- c(1,1,1,1)
trans.rate <- TransMatMakerGeoHiSSE(hidden.traits=1, make.null=TRUE)
trans.rate.mod <- ParEqual(trans.rate, c(1,2))
mod3 <- GeoHiSSE(phy = phy, data = sim.dat, f=c(1,1,1),
turnover=turnover, eps=eps,
hidden.states=TRUE, trans.rate=trans.rate.mod,
turnover.upper=100, trans.upper=10)Finally, if we want to fit a GeoHiSSE model we would do the following:
## Model 4. GeoHiSSE model with 1 hidden trait, range-dependent diversification.
turnover <- c(1,2,3,4,5,6)
eps <- c(1,1,1,1)
trans.rate <- TransMatMakerGeoHiSSE(hidden.traits=1)
trans.rate.mod <- ParEqual(trans.rate, c(1,2))
mod4 <- GeoHiSSE(phy = phy, data = sim.dat, f=c(1,1,1),
turnover=turnover, eps=eps,
hidden.states=TRUE, trans.rate=trans.rate.mod,
turnover.upper=100, trans.upper=10)We will also show how to fit a complementary set of models that remove the cladogenetic effect entirely, such that all changes occur along branches (i.e., anagenetic change). This requires the removal of the turnover rate for lineages in the widespread range and ensuring that range contraction is distinct from the extinction of endemics:
## Model 5. MuSSE-like model with no hidden trait, no cladogenetic effects.
turnover <- c(1,2,0)
eps <- c(1,1)
trans.rate <- TransMatMakerGeoHiSSE(hidden.traits=0, make.null=FALSE,
separate.extirpation = TRUE)
trans.rate.mod <- ParEqual(trans.rate, c(1,2))
trans.rate.mod <- ParEqual(trans.rate.mod, c(2,3))
mod5 <- GeoHiSSE(phy = phy, data = sim.dat, f=c(1,1,1),
turnover=turnover, eps=eps,
hidden.states=FALSE, trans.rate=trans.rate.mod,
turnover.upper=100, trans.upper=10, sann=FALSE,
assume.cladogenetic = FALSE)An explicit three-state MuSSE/MuHiSSE model can, and probably
should, be included in the set of models. This can be done by
using the MuHiSSE() function. The details for doing so can
be found in the Running a Multistate HiSSE model vignette.
Computing Akaike Weights.
Akaike weights are important to evaluate the relative importance of each of the models to explain the variation observed in the data. This quantity takes into account pennalties associated to the number of free parametes.
Models with higher weight show better fit to the data and, as a result, have more weight when performing model averaging (see below).
To compute model weight we can use one of the functions of the package. This will work with both HiSSE and GeoHiSSE objects.
load( "geohisse_new_vignette.Rsave" )
GetAICWeights(list(model1 = mod1, model2 = mod2, model3 = mod3, model4 = mod4), criterion="AIC")## model1 model2 model3 model4
## 0.634719404 0.097069174 0.263448130 0.004763292
## As the number of models in the set grows, naming each model in the set can become hard.
## So one can use a list (created by some automated code) as an input also:
list.geohisse <- list(model1 = mod1, model2 = mod2, model3 = mod3, model4 = mod4)
GetAICWeights(list.geohisse, criterion="AIC")## model1 model2 model3 model4
## 0.634719404 0.097069174 0.263448130 0.004763292Model averaging and plotting.
Now we can model average the results. Note that this step will reflect the Akaike model weights that we computed above.
For this we need first to perform a marginal reconstruction for each of the models in the set. This will reconstruct the hidden states at the nodes of the phylogeny. Then we can use this information to compute the model average for the rates.
These can take a while to run. We will load the results of previous analyses. Uncomment the code below to perform the reconstructions.
recon.mod1 <- MarginReconGeoSSE(phy = mod1$phy, data = mod1$data, f = mod1$f,
pars = mod1$solution, hidden.states = 1,
root.type = mod1$root.type, root.p = mod1$root.p,
AIC = mod1$AIC, n.cores = 4)
recon.mod2 <- MarginReconGeoSSE(phy = mod2$phy, data = mod2$data, f = mod2$f,
pars = mod2$solution, hidden.states = 1,
root.type = mod2$root.type, root.p = mod2$root.p,
AIC = mod2$AIC, n.cores = 4)
recon.mod3 <- MarginReconGeoSSE(phy = mod3$phy, data = mod3$data, f = mod3$f,
pars = mod3$solution, hidden.states = 2,
root.type = mod3$root.type, root.p = mod3$root.p,
AIC = mod3$AIC, n.cores = 4)
recon.mod4 <- MarginReconGeoSSE(phy = mod4$phy, data = mod4$data, f = mod4$f,
pars = mod4$solution, hidden.states = 2,
root.type = mod4$root.type, root.p = mod4$root.p,
AIC = mod4$AIC, n.cores = 4)
## Load previous results:
load( "geohisse_recons_new_vignette.Rsave" )Now that we have the AIC associated with each model and their reconstruction across the nodes of the tree we can compute the model average:
recon.models <- list(recon.mod1, recon.mod2, recon.mod3, recon.mod4)
model.ave.rates <- GetModelAveRates(x = recon.models, type = "tips")The result of the reconstrution is a matrix with the parameter
estimates for each of the tips species averaged over all models. Note
that for the GeoSSE model there is no “extinction” parameter associated
with widespread (01) lineages. Also not that one can change the type of
model averaging (between tips, nodes, and both) when callin the
GetModelAveRates function.
head( model.ave.rates )## taxon state.00 state.11 state.01 turnover net.div speciation extinct.frac
## 1 sp1 1 0 0 0.2398136 0.1543508 0.1970822 0.2168219
## 2 sp9 0 1 0 0.2405023 0.1547893 0.1976458 0.2168219
## 3 sp10 0 1 0 0.2405269 0.1548054 0.1976662 0.2168219
## 4 sp18 0 1 0 0.2408404 0.1550096 0.1979250 0.2168219
## 5 sp21 0 1 0 0.2407796 0.1549700 0.1978748 0.2168219
## 6 sp29 1 0 0 0.2398100 0.1543486 0.1970793 0.2168219
## extinction
## 1 0.04273139
## 2 0.04285647
## 3 0.04286077
## 4 0.04291541
## 5 0.04290481
## 6 0.04273072Finally, we can plot the use the resulting data matrix to make a plot of the results.
plot.geohisse.states(x = recon.models, rate.param = "net.div", type = "fan",
show.tip.label = FALSE, legend = FALSE)## [1] "Using default colors: white (state 1), black (state 2), and yellow (state 0)."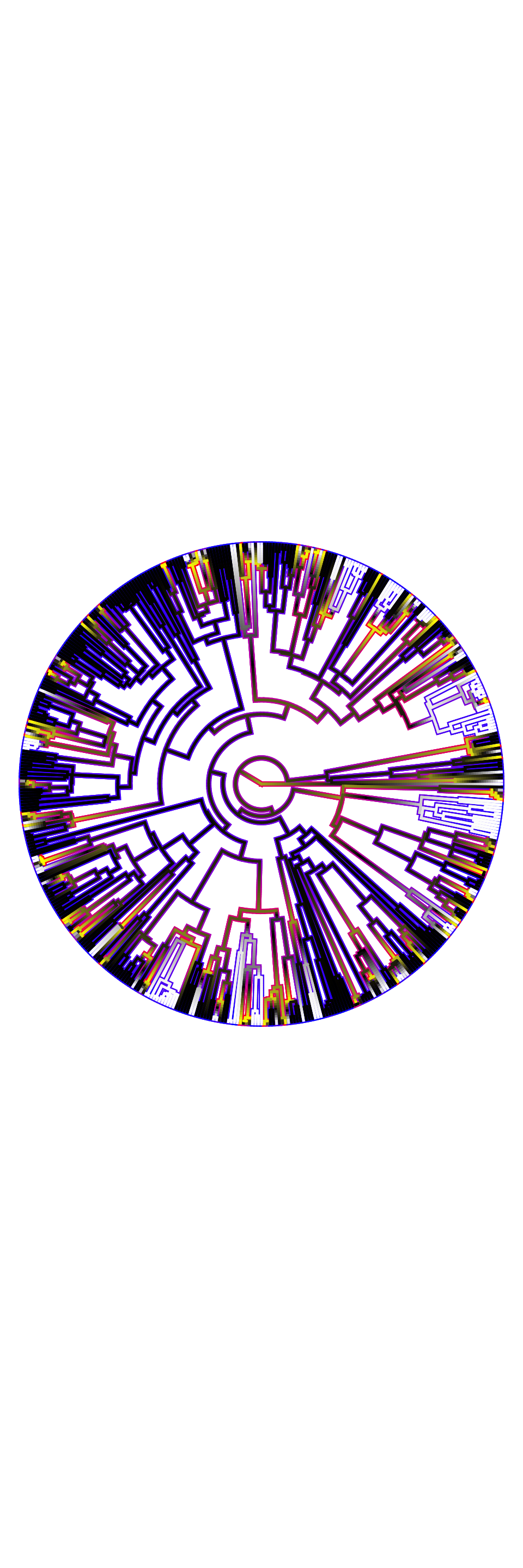
## $rate.tree
## Object of class "contMap" containing:
##
## (1) A phylogenetic tree with 500 tips and 499 internal nodes.
##
## (2) A mapped continuous trait on the range (0.15419, 0.582421).
##
##
## $state.tree
## Object of class "contMap" containing:
##
## (1) A phylogenetic tree with 500 tips and 499 internal nodes.
##
## (2) A mapped continuous trait on the range (0, 2.002).