Type I errors, Model rejection, & HiSSE vs. FiSSE

Jeremy M. Beaulieu & Brian C. O’Meara

All you really need to know for the moment is that the universe is a lot more complicated than you might think, even if you start from a position of thinking it’s pretty damn complicated in the first place. – Douglas Adams

Introduction

A important concern regarding SSE models (State Speciation and Extinction; Maddison et al 2007) was recently raised by Rabosky and Goldberg (2015). They demonstrated that if a tree evolved under a heterogeneous branching process that is completely independent from the evolution of the focal character, SSE models will almost always return high support for a model of trait-dependent diversification. From an interpretational stand point, this is troubling. However, a common misconception is that SSE models are typical models of trait evolution like those in, say Pagel (1994) or O’Meara et al. (2006), which simply maximize the probability of the observing trait information at the tips, given the tree and model – the tree certainly affects the likelihood of observing the configuration of trait data at the tips, but that is the only way it enters the calculation. An SSE model, on the other hand, actually jointly maximizes the probability of the observed states at the tips and the observed tree, given the model. This is an important distinction because if a tree violates a single regime birth–death model due to mass extinction events, trait-dependent speciation or extinction, maximum carrying capacity, or whatever, then even if the tip data are perfectly consistent with a simple transition model, the tip data plus the tree are not. In such cases BiSSE is very wrong in assigning rate differences to a neutral trait, but a simple equal rates diversification model is not correct either. This leaves practitioners in quite the bind because the “right” model isn’t something that can be tested in BiSSE. This is elaborated on in the discussion of Beaulieu and O’Meara (2016).

Nevertheless, these results have created concerns among empiricists with respect to SSE models. There are reasons to be concerned, but a deeper issue is misinterpretation of hypothesis testing. First, rejecting the null model does not imply that the alternative model is the true model. It simply means that the alternative model fits less badly. Second, in biological examples, including many of those used for testing Type I error, it isn’t Type I error at all. It is simply rejecting model A, for model B, when model C is true. There is a mnemonic for remembering Type I versus Type II error that was recently making the rounds on social media – the story of the boy that cried wolf. When he first cried wolf, but there was no wolf, he was making a Type I error – that is, falsely rejecting the null of a wolf-free meadow. When the townspeople later ignored him when there was actually a wolf, they were making a Type II error. If the sheep were instead perishing in a snowstorm, and the only options for the boy are to yell “no wolf!” or “wolf!” it is not clear what the best behavior is – “no wolf” implies no change in sheep mortality rates from when they happily gambol in a sunny meadow, even though they have begun to perish, while “wolf” communicates the mortality increase but has the wrong mechanism. It is the same here when looking at a tree coming from an unknown but complex empirical branching model and trying to compare a constant rate model (“no wolf”) with a trait-dependent (“wolf”), age-dependent (“bear”), or density-dependent model (“piranha”).

The major problem in our view is that ever since SSE models became standard practice, we have relied a bit too heavily on rather trivial “null” models (i.e., equal rates diversification) to compare against models of trait dependent diversification. Given the rich complexity of processes affecting diversification (mass extinctions, local extinctions, competition, biogeographic changes, etc.) and trait evolution (varying population size, selection pressure, available variation, etc.), a comparison of “one rate for all time for all traits” vs “something a bit more complex” will usually return the latter. A fairer comparison would involve some sort of “null” model that contains the same degree of complexity in terms of numbers of parameters for diversification, but is also independent of the evolution of the focal character, to allow for comparisons among any complex, trait-dependent models of interest.

In Beaulieu and O’Meara (2016), we proposed two such models. These character-independent (CID) models explicitly assume that the evolution of a binary character is independent of the diversification process without forcing the diversification process to be constant across the entire tree. The first model, which we refer to as “CID-2”, contains four diversification process parameters (two speciation and two extinction rates) that account for trait-dependent diversification solely on the two states of an unobserved, hidden trait (which could be, in reality, a set of traits, environmental conditions, etc. – just something that leads to two different rates). In this way, CID-2 contains the same amount of complexity in terms of diversification as a BiSSE model. The second model, which we refer to as “CID-4” contains the same number of diversification parameters as in the general HiSSE model that are linked across four hidden states. Practical details on how to set them up in hisse can be found in the Running HiSSE vignette.

In our HiSSE paper, we conducted a series of simulations to assess the behavior of including these character-independent models. Specifically, we generated species tree evolved under complex, and sometimes unknown, diversification processes, and focal traits being evolved on them independent of the diversification process. In all cases, when the generating model was consistent with character-independent diversification, we found our CID models substantially reduced the evidence favoring the trait-dependent models (i.e., BiSSE and HiSSE). In fact, we even tested what we referred to as a “worst-case” scenario, which involved simulating trees where the speciation rate evolved in a heterogeneous manner, and again simulating a neutral binary character onto them. Without our CID models being included in the set of models under evaluation, BiSSE had substantial support nearly 80% of the time. However, when we added just the CID-2 model, only 1% of those same data sets showed substantial support for BiSSE. When we tested the full set, which included both HiSSE and CID-4, in addition to BiSSE and CID-2, roughly 16% of the time either the BiSSE or HiSSE model had substantial support (though this is still above the 5% nominal eror rate). Comparing the parameter estimates from those data sets indicated that the differences in the parameter estimates among the different observed states were minimal. Thus, even if a trait-dependent model were to be chosen, the parameter estimates would suggest any rates differences are likely biologically insignificant.

HiSSE vs. FiSSE

Recently, Rabosky and Goldberg (2017) proposed a simple nonparametric test for determining the effect of a binary character on rates of diversification. The performance of FiSSE is encouraging from the standpoint of model rejection – under a range of very difficult, and often extreme scenarios, FiSSE can differentiate between scenarios of trait-dependent and trait-independent diversification fairly well (see their Fig. 6). For good measure, they also compared the performance of our parametric, process-based HiSSE under these same scenarios, and found that while the inclusion of our CID-2 model reduced the overall “false positive” rate of BiSSE, the use of BiSSE + CID-2 + HiSSE resulted in nine of 34 trait-independent diversification scenarios (referred to as SDD in Rabosky and Goldberg 2017) having “false-positive” rates in excess of 25%.

While we do not dispute the results as they are presented in Rabosky and Goldberg (2017), we do feel that the HiSSE model comparisons were not conducted quite in the manner in which we intended. If even experts in this area missed this, it suggests we need to do a better job explaining CID models. As stated above, the CID-2 model was derived to contain the same amount of complexity in terms of diversification as a BiSSE model. That is, our CID-2 has two speciation rates (\(\lambda_{0A} = \lambda_{1A}\), \(\lambda_{0B} = \lambda_{1B}\)) and two extinction rates (\(\mu_{0A} = \mu_{1A}\), \(\mu_{0B} = \mu_{1B}\)), as does BiSSE (\(\lambda_0\), \(\lambda_1\), \(\mu_0\), \(\mu_1\)). However, when HiSSE is included, it is much more complex than either BiSSE or CID-2. So, again, if the complexity of the process that generated the tree exceeds that of the CID-2 model in any of the non-SDD scenarios, then we should expect the more complex HiSSE model to fit better for precisely same reasons as described above. In other words, the model in the set that best matches the complexity of the scenario is in fact a trait-dependent model of diversification. This is precisely why we also derived the CID-4 model, which equals the same complexity as HiSSE. Like HiSSE, which has four speciation rates (\(\lambda_{0A}\), \(\lambda_{1A}\), \(\lambda_{0B}\), \(\lambda_{1B}\)) and extinction rates (\(\mu_{0A}\), \(\mu_{1A}\), \(\mu_{0B}\), \(\mu_{1B}\)), the CID-4 also has four speciation rates (\(\lambda_{0A} = \lambda_{1A}\), \(\lambda_{0B} = \lambda_{1B}\), \(\lambda_{0C} = \lambda_{1C}\), \(\lambda_{0D} = \lambda_{1D}\)) and four extinction rates (\(\mu_{0A} = \mu_{1A}\), \(\mu_{0B} = \mu_{1B}\), \(\mu_{0C} = \mu_{1C}\), \(\mu_{0D} = \mu_{1D}\)). Importantly, while these two models are equally complex with respect to diversification “rate classes”, they also have entirely different interpretations with respect to whether or not they are associated with changes in a focal character state.

Reanalysis of Rabosky and Goldberg (2017) with CID-4 in the set

First, a brief note about the trait-independent scenarios (i.e., no SDD) presented in Rabosky and Goldberg (2017). Usefully, these represent some of the most extreme cases we have encountered when testing the performance of HiSSE. For example, out of the 34 trait-independent scenarios, 27 were trees either simulated (19 of the 27 scenarios) to have a total height of 1, or were empirical trees (8 of the 27) that were rescaled so that their total height is 1. In most uses of *SSE models, tree height is usually in units of millions of years and so usual tree heights are dozens to even hundreds of years. While the only effect of this should be a linear scaling of rates on the height 1 trees compared to chronograms, with no real effect other than difficulty interpreting units of the rates, in practice given numerical integration this can lead to issues. Analogously:

a <- 1e-100
a == 2 * a
## [1] FALSE
b <- 1e-1000
b == 2 * b
## [1] TRUE

The tests of equality are the same, and in each case the number on the left is half that on the right, but the second one shows TRUE due to numerical underflow. Of course, this is a numerical issue with a solution. Starting with version 1.8.3 the optimization defaults to a bounded subplex routine where we set the upper bounds to be reasonable with respect what we think is biologically realistic. For example, the upper bound on turnover (i.e., \(\lambda_i + \mu_i\)) is set to 10,000, which assumes, on average, one event every 100 years on a chronogram in units of millions of years. For extinction fraction, (i.e., \(\mu_i / \lambda_i\)), the upper limit is set to 3, which, in our view, far exceeds the extinction fraction of any observable extant clade. We also now include a new setting, ode.eps, that sets the tolerance for the integration at the end of a branch. Essentially, if the sum of the probability of \(D_i\) is less than this tolerance, then it assumes the results are unstable and discards them. For the present purposes, however, the ode.eps was set to zero.

Using code helpfully provided by Rabosky and Goldberg (2017), we refit and summarized the same BiSSE + CID-2 + HiSSE model set as described in the paper. When evaluating these models using our updated optimization routine we found that with the trait-independent scenarios we actually do slightly worse than described in the original study. Of the 34 non-SDD, 13 had “false positive” rates that exceeded 25%, which we suggest is due to optimization failures in the previous version of HiSSE. But, generally, our results hew rather closely to Rabosky and Goldberg (2017). The BiSSE + CID-2 + HiSSE model set still shows improved power over FiSSE with scenarios of trait-dependent diversification, and with trait-independent diversification the same data sets that performed poorly in their analysis remain poor performers in our reanalysis (Fig. 1).

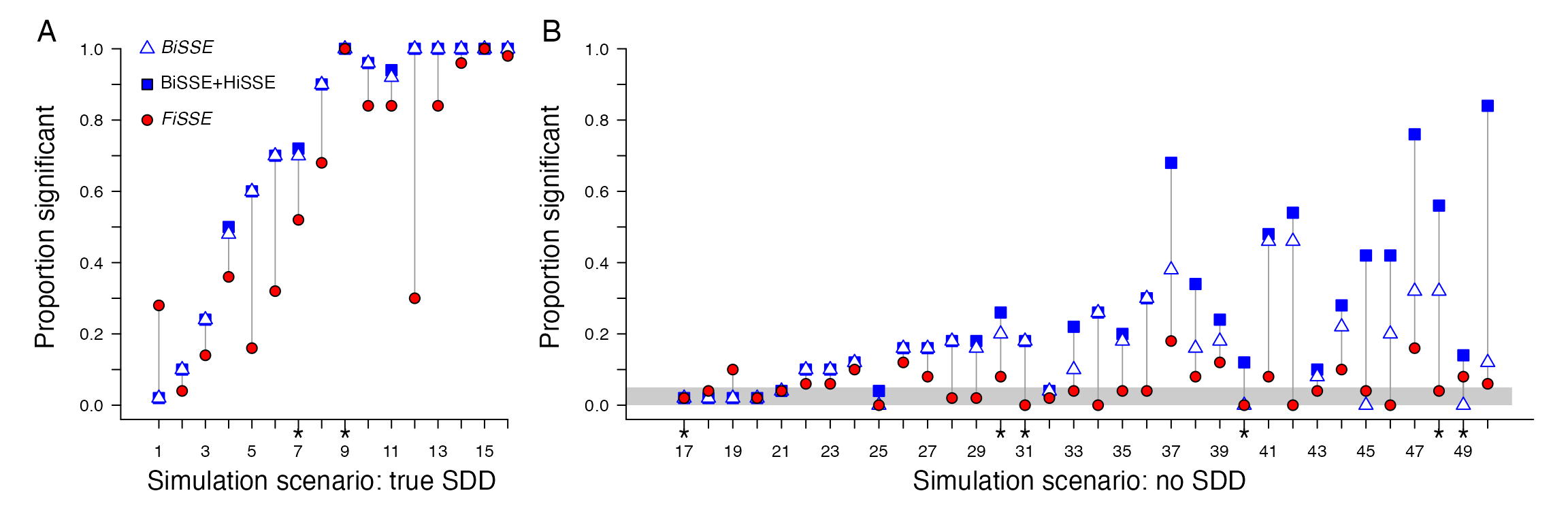
Reanalysis of the Rabosky and Goldberg (2017) using a bounded subplex optimization routine. Overall, the results from the updated optimization routine closely follow those presented in the original study.

Reanalysis of the Rabosky and Goldberg (2017) using a bounded subplex optimization routine. Overall, the results from the updated optimization routine closely follow those presented in the original study.

We then fit a fourth model, CID-4, and reevaluated the “false positive” rate for a model set that now includes BiSSE + CID-2 + HiSSE+ CID-4. Again, the use of CID-4 is to provide a model that has the same complexity in terms of diversification as HiSSE, but allows for an entirely different interpretation with respect to whether or not they are associated with changes in a focal character state. It is something we suggest anyone use when running HiSSE, especially if the question is about model rejection. The HiSSE model used by Rabosky and Goldberg (2017) included three transition rates, rather than the full eight transition rates that HiSSE allows. We therefore used the trans.type="three.rate" when running the hisse.null4() function, so the two models have exactly the same number of parameters.

When CID-4 is included in the model set, the power to detect trait-dependent diversification remains completely unchanged, and exhibits greater statistical power compared to FiSSE (Fig. 2A). For the trait-independent diversification scenarios (Fig. 2B), the inclusion of CID-4 in the model set almost always results in a reduction in the “false positive” rate for each scenario. In several instances the drop in spurious support for a trait-dependent diversification model was substantial. For example, scenario 50, which involves a density-dependent tree and fast evolving neutral trait (i.e., q=10), went from 84% of the data sets supporting a trait-dependent model of diversification, to only 8% support when CID-4 is included in the set.

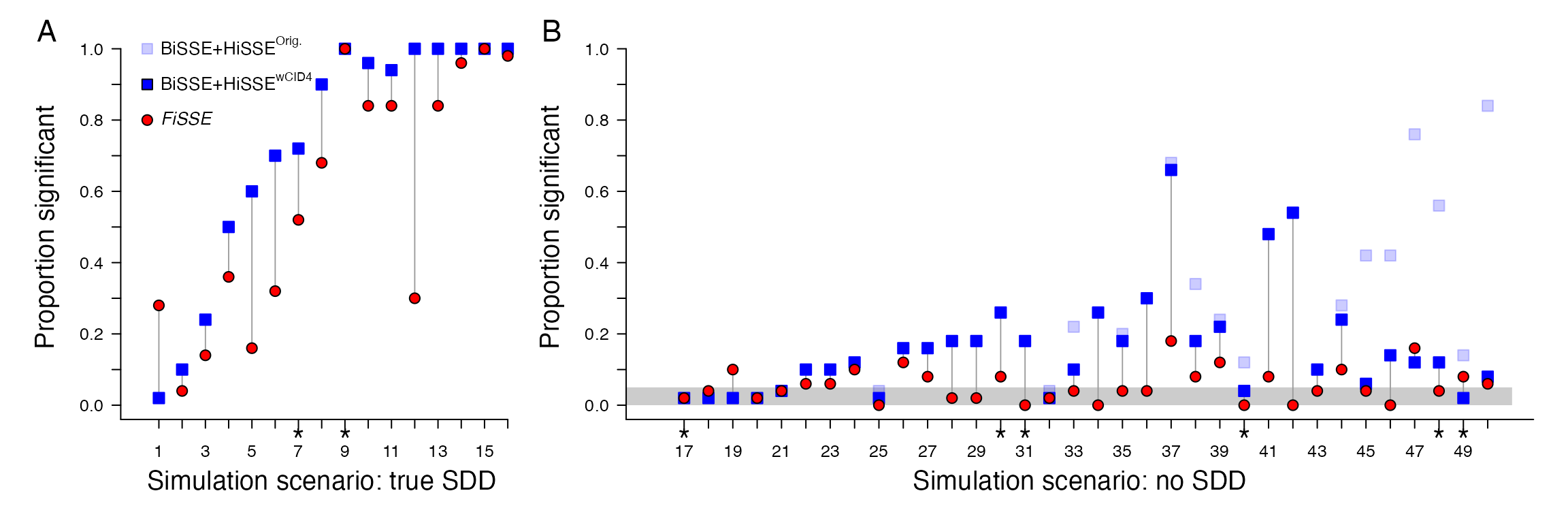
Reanalysis of the Rabosky and Goldberg (2017) when our 4-state character independent model, CID-4, is included in the model set (dark blue boxes). When compared against the fit of BiSSE, CID-2, and HiSSE, the (A) power to detect the trait-dependent diversification remains unchanged. For the trait-independent scenarios (B), there is almost always a reduction in the 'false positive' rate (as indicated by the difference in the position of the light blue and dark blue boxes), and in many cases the reduction is substantial.

Reanalysis of the Rabosky and Goldberg (2017) when our 4-state character independent model, CID-4, is included in the model set (dark blue boxes). When compared against the fit of BiSSE, CID-2, and HiSSE, the (A) power to detect the trait-dependent diversification remains unchanged. For the trait-independent scenarios (B), there is almost always a reduction in the ‘false positive’ rate (as indicated by the difference in the position of the light blue and dark blue boxes), and in many cases the reduction is substantial.

There are, however, three scenarios that remain problematic for HiSSE (scenarios 37, 41, and 42; Fig. 2B). Interestingly, all three were generated from the same empirical tree, which is a large supertree of corals. Branch lengths in this empirical tree were rescaled from their original units so that the total height was 1. Furthermore, with scenario 37, we are conflicted as to whether this truly represents a trait-independent model of diversification. As described by Rabosky and Goldberg (2017), this data set is a “neutral trait simulated on an empirical tree, with a rapidly diversifying clade then fixed (manually) to a single value of the trait.” In other words, a clade at, or at least near, a major shift in diversification was fixed to a particular state regardless of the the process the character was simulated under. At best, we would agree that this scenario represents a special case more in line with the “Darwin scenario”” discussed in detail by Maddison and FitzJohn (2015). These special cases reflect either a single pseudoreplicated event or ascertainment bias of a much larger clade, and thus should not statistically have enough power to be properly be defined as a trait-dependent diversification. In any case, clearly scenarios 41 and 42 remain problematic for HiSSE.

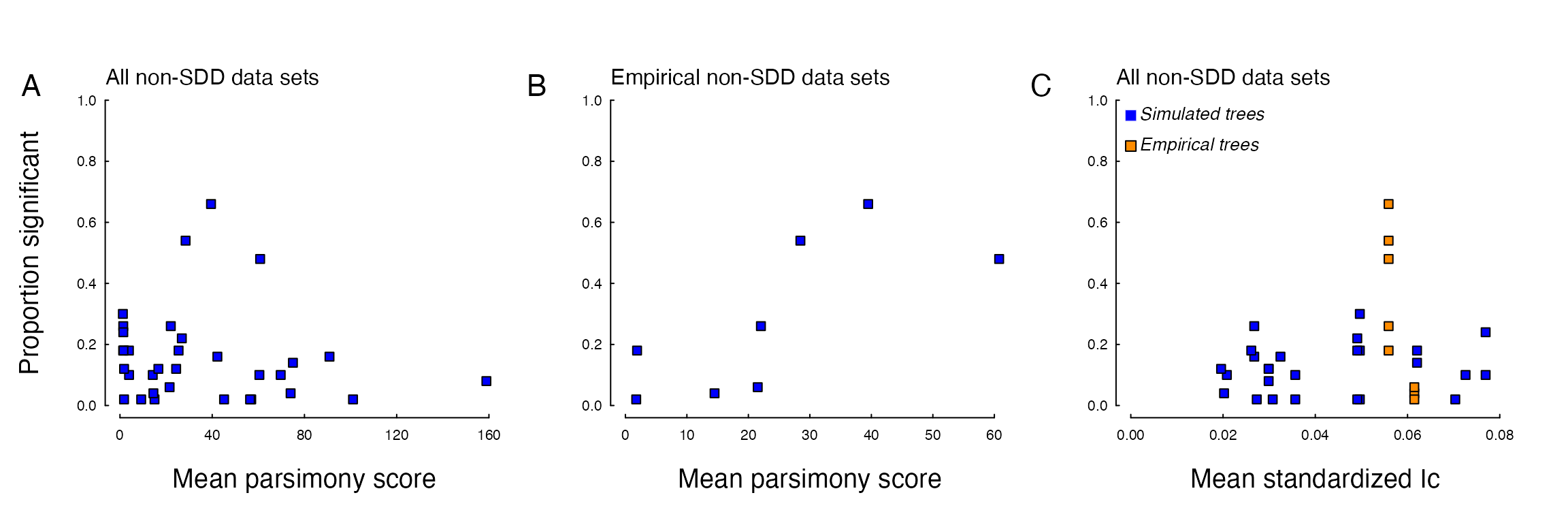
Relationship between parsimony score of the simulated character and the proportion of data set that returned spurious support for trait-dependent diversification. (A) Across all trait-independent scenarios, there was no trend, but when examining only the scenarios that modified empirical trees (B), there was a postive trend between parsimony score and the 'false positive' rate. (C) We also found no relationship between Colless' Index (Ic), which we standardized by the Ic of completely pectinate tree with the same number of tips, and the 'false positive' rate, and the empirical trees (orange boxes) do not stand out as being overly balanced or imbalanced relative to the simulated trees (blue boxes).

Relationship between parsimony score of the simulated character and the proportion of data set that returned spurious support for trait-dependent diversification. (A) Across all trait-independent scenarios, there was no trend, but when examining only the scenarios that modified empirical trees (B), there was a postive trend between parsimony score and the ‘false positive’ rate. (C) We also found no relationship between Colless’ Index (Ic), which we standardized by the Ic of completely pectinate tree with the same number of tips, and the ‘false positive’ rate, and the empirical trees (orange boxes) do not stand out as being overly balanced or imbalanced relative to the simulated trees (blue boxes).

We also closely examined each of the data sets from the trait-independent scenarios and found nothing obvious about them that may be useful predictors of the “false positive” rate. For example, the parsimony score, which provides a coarse indication of the minimum number of changes in the discrete character, did not predict the percentage of the spurious support for a trait-dependent model of diversification. We do note that when we separated the scenarios by whether or not the tree was generated through simulation or by modifying existing empirical trees (Fig. 3B), there was a clear positive trend, though with only six data points it is difficult to conclude whether such a pattern is real or simply coincident. We also examined the relationship between a standardized measure of tree balance and the false positive rate (Fig. 3C), and again we found no obvious trend, with the empirical trees neither being overly balanced, nor imbalanced, relative to the simulated trees.

Taken together, HiSSE actually performs reasonably well for hypothesis rejection when a model set including appropriate nulls is evaluated. These results also demonstrate how important it is, when the goal of a study is simply model rejection, that null models are included with at least a fighting chance. We also encouraged by the performance of HiSSE considering that the simulation scenarios put together by Rabosky and Goldberg (2017) are rather extreme and unlikely to ever occur in an empirical setting. Of course, the failure of several scenarios involving a particular empirical tree (i.e., coral supertree) does suggest that there may be other empirical data sets prone to spuriously providing strong evidence for trait-dependence diversification.

Suggestions

In Beaulieu and O’Meara (2016), which describes the details of our HiSSE approach, we call for focusing more on parameter estimation over model rejection. However, at the urging of a reviewer, we did include analyses of model rejection. Much of the discussion of SSE models has centered on Type I error (or related things incorrectly called Type I error). Skepticism towards models is of tremendous importance, but as a field we now focus too much on rejecting trivial nulls. This feels scientific because it is how many of us were taught statistics. Meanwhile, in the field of statistics, our colleagues are looking on in horror. A useful guide is summary of the American Statistical Association’s Statement on Statistical Significance and P-Values; also see the actual publication (Wasserstein & Lazar, 2016). It has six principles:

  1. P-values can indicate how incompatible the data are with a specified statistical model.
  2. P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
  3. Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
  4. Proper inference requires full reporting and transparency.
  5. A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
  6. By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.

In certain areas of biology, we seem to stop after rejecting a null model that we already knew was false, though to be fair it is useful to get information about whether or not an effect might be present. However, we suggest scientists go beyond this to actually look at parameter estimates. Suppose we find the diversification rate in state 1 is higher than state 0. Is it 0.0001% higher, or is it 300% higher? The answer could have biologically very different implications. Rather than just rejecting nulls, we suggest using HiSSE to do multimodel inference – compare a variety of models, look at weight for each, and make biological conclusions based on these models and their parameter estimates. The plotting functions in HiSSE were implemented specifically to promote this approach even when one cannot compare states directly (the diversication rate in 0D in a CID4 model does not easily map to a 0A or 0B rate in a HiSSE model), averaged rates at tips and nodes can be used to find estimates of rates, incorporating model uncertainty. See the Running HiSSE vignette for more details on how to do this.

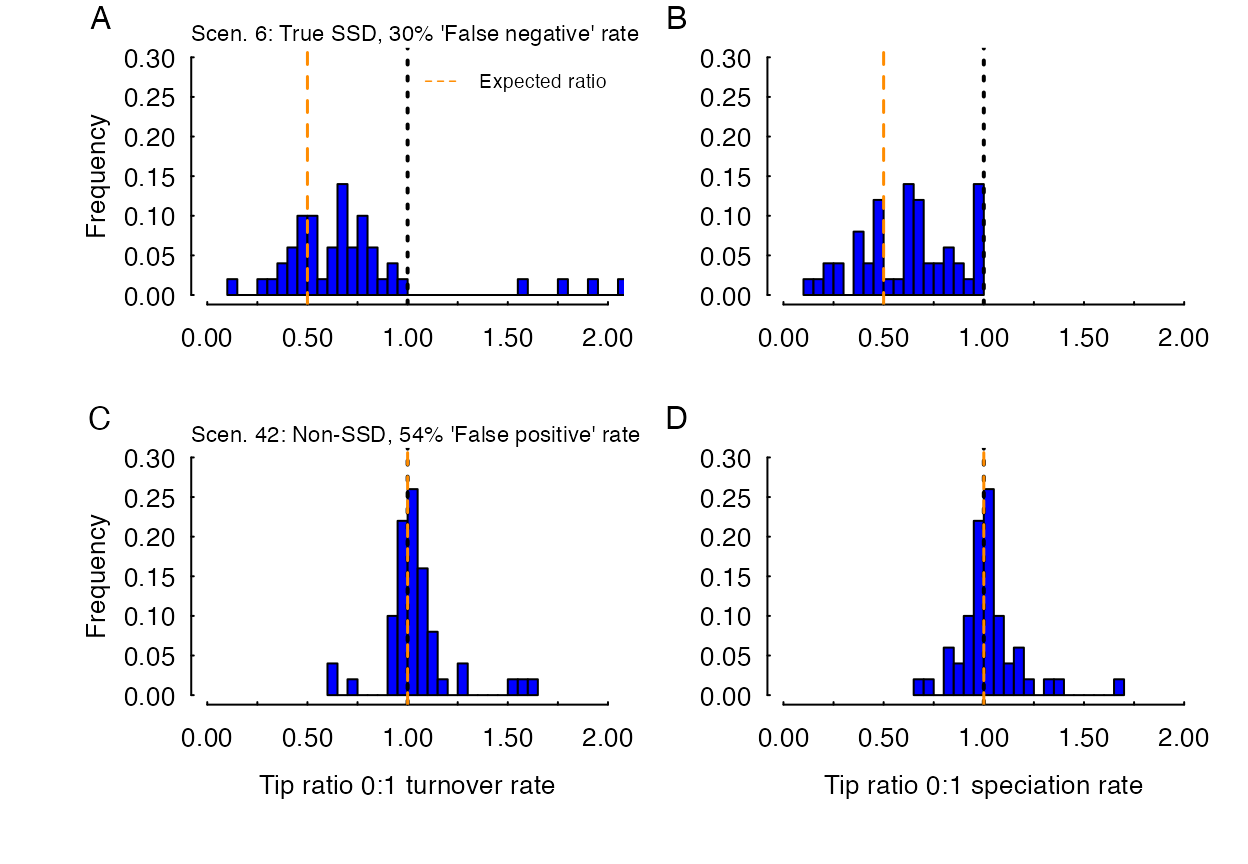
Model-averaged parameter estimates of turnover and speciation from two scenarios, a true SSD scenario (A,B) where our HiSSE model set showed high 'false negative' rates (i.e., failed to reject a trait-independent scenario), and a non-SSD scenario (C,D) which exhibited a 54% false-positive rate. In the case of the non-SSD scenario, it clearly shows that despite the poor performance of from a model rejection perspective, examining the the model parameters would indicate that on average, there are no differences in diversification rates among observed states. The dashed orange line represents the expected ratio to be compared against a ratio of difference in diversification rates between state 0 and 1 denoted by the dotted black line.

Model-averaged parameter estimates of turnover and speciation from two scenarios, a true SSD scenario (A,B) where our HiSSE model set showed high ‘false negative’ rates (i.e., failed to reject a trait-independent scenario), and a non-SSD scenario (C,D) which exhibited a 54% false-positive rate. In the case of the non-SSD scenario, it clearly shows that despite the poor performance of from a model rejection perspective, examining the the model parameters would indicate that on average, there are no differences in diversification rates among observed states. The dashed orange line represents the expected ratio to be compared against a ratio of difference in diversification rates between state 0 and 1 denoted by the dotted black line.

We can demonstrate the importance of examining model parameters over model rejection by summarizing the ratios in diversification between observed states 0 and 1 for two scenarios in which HiSSE performed poorly from a model rejection perspective. We have now added two new functions, GetModelAveTipRates() and GetModelAveNodeRates(), which provide model-averaged rates while also accounting for uncertainty in both states for tips and nodes when provided a list of reconstructions (identical to set up plot.hisse.states() – see Running HiSSE vignette). Take, for instance, the true-SSD scenario 6, where 30% of the data sets failed to “reject” the null of a non-SSD interpretation (i.e, a “false negative” rate). The ratio of the turnover rate of state 0 to state 1 (which is average across the hidden state), however, was correctly estimated to be less than 1 (simulation had speciation for state 0 50% that of state 1) in all but four data sets (median tip ratio turnover was 0.67; Fig. 4A). In the four cases in which the state 0 had a higher turnover rate than state 1, and hence a tip ratio >1, was due to highly inaccurate estimates of extinction for state 0, which inflated the turnover rate. Indeed, when examining the speciation rate alone, all data sets returned a model-averaged ratio that was less than 1 (median tip ratio for speciation was 0.63; Fig. 4B).

An even more striking example comes from the non-SSD scenarios. Scenario 42, which exhibited one of the worst “false positive” rates even after accounting for CID-4 in the model set had model-average tip ratio distribution that was centered on 1 (the median tip ratio for turnover and speciation was 1.01 and 1.00, respectively), as it should, indicating no rate differences among the observed states. Of course, when we examined the limits of these results by determining the number of data sets that exceeded 10% on either side of 1, only 70% of all data sets fall within this range. So, it is possible that spuriously significant rate differences may still be returned. However, the important point is that when we examine the model parameters, clearly the situation is not as dire as it would seem had we only relied on which model fit best.

References

Beaulieu, J.M., and B.C. O’Meara. (2016). Detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Syst. Biol. 65:583-601.

Maddison, W.P., P.E. Midford, and S.P. Otto. (2007). Estimating a binary characters effect on speciation and extinction. Syst. Biol. 56:701-710.

Maddison, W.P., and R. FitzJohn. (2015). The unsolved challenge to phylogenetic correlation tests for categorical characters. Syst. Biol. 64:127-136.

Pagel, M. (1994). Detecting correlated evolution on phylogenies: a general method for the comparative analysis of discrete characters. Proc. Roy. Soc., B. 255:37-45.

O’Meara, B.C., C. Ane, M.J. Sanderson, and P.C Wainwright. (2006). Testing for different rates of continuous trait evolution using likelihood. Evolution 60:922-933.

Rabosky, D.L., and E.E. Goldberg. (2015). Model inadequacy and mistaken inferences of trait-dependent speciation. Syst. Biol. 64:340-355.

Rabosky, D.L., and E.E. Goldberg. (2017). FiSSE: a simple non-parametric test for the effects of a binary character on lineage diversification rates. In press, Evolution.

Wasserstein, R.L., and N. A. Lazar. (2016). The ASA’s Statement on p-Values: Context, Process, and Purpose. The American Statistician, 70:2, 129-133. http://dx.doi.org/10.1080/00031305.2016.1154108